If an element outside the set is produced, then the operation is not ___. D) the set of natural numbers is not closed under the operation of subtraction because when you subtract one natural number from another, you don’t always get another natural number.
Which Set Of Numbers Is Closed Under Subtraction. System of whole numbers is not closed under subtraction, this means that the difference of any two whole numbers is not always a whole number. Which set is closed under subtraction? This set is often in folders with. For example, the closure under subtraction of the set of natural numbers, viewed as a subset of the real numbers, is the set of integers.
The Closure Property Of Real Numbers - Video & Lesson Transcript | Study.com From study.com
Related Post The Closure Property Of Real Numbers - Video & Lesson Transcript | Study.com :
Actually, when you subtract odd numbers, you always get an even number! A set is ___ (under an operation) if the operation always produces an element of the same set. Natural numbers are closed under division. If you subtract two whole numbers, you do not always get a whole number.
Whole numbers are not a closed set under subtraction:
A/b + c/d = (ad+bc)/bd, so closed under addition. At some point, people were confronted with the problem of having to divide one thing among more than one person. If an element outside the set is produced, then the operation is not ___. −5 is not a whole number (whole numbers can�t be negative) so: As an opposite example, negative numbers are a closed set under addition. Irrational numbers $$\mathbb{i}$$ we have seen that any rational number can be expressed as an integer, decimal or exact decimal number.
Source: slideplayer.com
D) the set of natural numbers is not closed under the operation of subtraction because when you subtract one natural number from another, you don’t always get another natural number. If an element outside the set is produced, then the operation is not ___. This is a general idea, and.
Source: slidetodoc.com
Thus, rational numbers are closed under addition, subtraction and multiplication. Natural numbers are closed under division. If we enlarge our set to be the integers
Source: chegg.com
As an opposite example, negative numbers are a closed set under addition. An important example is that of topological closure. Which of the following sets are closed under subtraction?
Source: youtube.com
System of whole numbers is not closed under subtraction, this means that the difference of any two whole numbers is not always a whole number. The natural numbers are closed under addition means that if i add two natural numbers, the sum will also be a natural number. At some point, people were confronted with the problem of having to divide one thing among more than one person.
Source: slideplayer.com
System of whole numbers is not closed under subtraction, this means that the difference of any two whole numbers is not always a whole number. For any two rational numbers a and b, (a+b),(a−b),(b−a) & (a×b) are all rational numbers. Thus, rational numbers are closed under addition, subtraction and multiplication.
Source: brainly.in
Click here to see full answer Which of the following sets are closed under subtraction? Two whole numbers the result is also a whole number, but if we try subtracting two such numbers it is possible to get a number that is not in the set.
Source: youtube.com
A/b + c/d = (ad+bc)/bd, so closed under addition. Click here to see full answer This means that rational numbers are.
Source: slideplayer.com
This is known as closure property for subtraction of whole numbers. The notion of closure is generalized by galois connection , and further by monads. Integers provide closure under subtraction, while whole numbers do not.
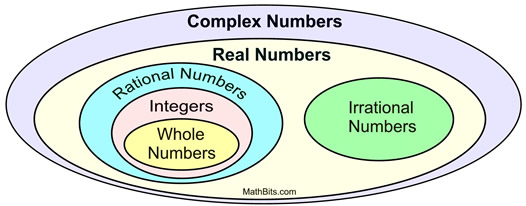Source: mathbitsnotebook.com
This is known as closure property for subtraction of whole numbers. As an opposite example, negative numbers are a closed set under addition. A/b + c/d = (ad+bc)/bd, so closed under addition.
Source: meritnation.com
Whole numbers are not closed under subtraction. For any two rational numbers a and b, (a+b),(a−b),(b−a) & (a×b) are all rational numbers. −5 is not a whole number (whole numbers can�t be negative) so:
Source: chegg.com
The notion of closure is generalized by galois connection , and further by monads. Irrational numbers $$\mathbb{i}$$ we have seen that any rational number can be expressed as an integer, decimal or exact decimal number. Click here to see full answer
Source: chegg.com
The rational numbers are closed not only under addition, multiplication and subtraction, but also division (except for $$0$$). The rational numbers are closed not only under addition, multiplication and subtraction, but also division (except for $$0$$). A/b + c/d = (ad+bc)/bd, so closed under addition.
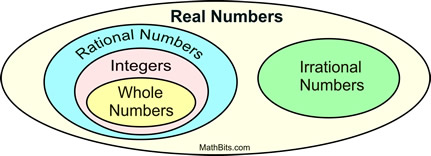Source: mathbitsnotebook.com
One can define the difference between $a$ and $b$, $a, b \in \mathbb n,$ in terms of the magnitude of the difference: Negative integers, integers and rational numbers are the sets of numbers among the choices given in the question that are closed under subtraction. For any two rational numbers a and b, (a+b),(a−b),(b−a) & (a×b) are all rational numbers.
Source: youtube.com
Operations under which a particular set is not closed require new sets of numbers: They are not closed under division because, for example, 1 , 0 ∈. Natural numbers are closed under division.
Source: brainly.in
A set is ___ (under an operation) if the operation always produces an element of the same set. So, the set of negative numbers is not closed to subtraction. This is known as closure property for subtraction of whole numbers.
Source: slideplayer.com
No, subtraction is not closed on the set of natural numbers. This set is often in folders with. One can define the difference between $a$ and $b$, $a, b \in \mathbb n,$ in terms of the magnitude of the difference:
Source: brainly.com
For any two rational numbers a and b, (a+b),(a−b),(b−a) & (a×b) are all rational numbers. A set is ___ (under an operation) if the operation always produces an element of the same set. Which of the following sets are closed under subtraction?
Source: study.com
Actually, when you subtract odd numbers, you always get an even number! Click here to see full answer So, if you try it with negative numbers and subtraction, you can quickly find examples where subtracting negative numbers gives a positive number as a result.
Source: studylib.net
System of whole numbers is not closed under subtraction, this means that the difference of any two whole numbers is not always a whole number. 4 − 9 = −5. Irrational numbers $$\mathbb{i}$$ we have seen that any rational number can be expressed as an integer, decimal or exact decimal number.
Source: youtube.com
At some point, people were confronted with the problem of having to divide one thing among more than one person. So, if you try it with negative numbers and subtraction, you can quickly find examples where subtracting negative numbers gives a positive number as a result. The notion of closure is generalized by galois connection , and further by monads.
Also Read :
