A set is closed under subtraction means if you can subtract any two numbers in the set and still have a number in the set as a result. Explanation integers are closed under subtraction which mean that subtraction of integers will also give integers.
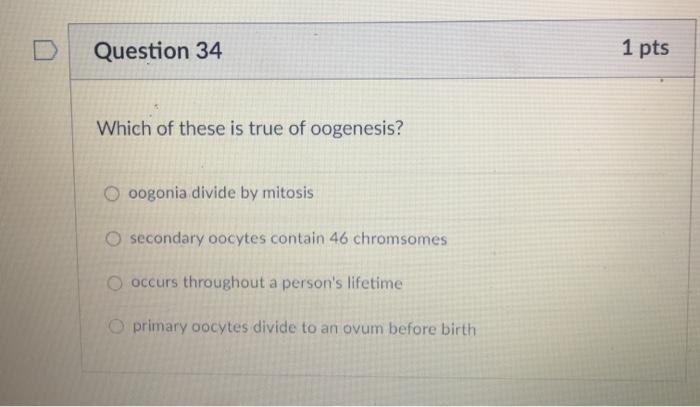
Which Set Is Closed Under Subtraction. The set that is not closed under subtraction is b) z. Set {0, 1} so this set is closed under multiplication. It�s a nice way of getting organized and. A set that is closed under an operation or collection of operations is said to satisfy a closure property.
![Solved] 1.Is The Set Of Rational Expressions Closed Under Subtraction?Explain P(X)/Q(X) - R(X)/S(X) = 2.Is The Set Of Rational Expressions Closed Un… | Course Hero](https://www.coursehero.com/qa/attachment/14590262/ “Solved] 1.Is The Set Of Rational Expressions Closed Under Subtraction?Explain P(X)/Q(X) - R(X)/S(X) = 2.Is The Set Of Rational Expressions Closed Un… | Course Hero”) Solved] 1.Is The Set Of Rational Expressions Closed Under Subtraction?Explain P(X)/Q(X) - R(X)/S(X) = 2.Is The Set Of Rational Expressions Closed Un… | Course Hero From coursehero.com
Related Post Solved] 1.Is The Set Of Rational Expressions Closed Under Subtraction?Explain P(X)/Q(X) - R(X)/S(X) = 2.Is The Set Of Rational Expressions Closed Un… | Course Hero :
Whole numbers are not closed under subtraction. This closure game is fun. −5 is not a whole number (whole numbers can�t be negative) so: Real numbers are closed under addition and multiplication.
Whole numbers are not closed under subtraction.
A set is closed under an operation if the results of that operation always lies in that set. A set is closed under an operation if the results of that operation always lies in that set. Explanation integers are closed under subtraction which mean that subtraction of integers will also give integers. For two rational numbers say x and y the results of addition, subtraction and multiplication operations give a rational number. So another way of saying the above statements is: Closure property of rational numbers under multiplication:
Source: meritnation.com
Often a closure property is introduced as an axiom, which is then usually called the axiom of closure. A set that is closed under an operation or collection of operations is said to satisfy a closure property. This closure game is fun.
Source: qa-all.com
We can say that rational numbers are closed under addition, subtraction and multiplication. The set of rational numbers is closed under addition, subtraction, multiplication, and division (division by zero is not defined) because if you complete any of these operations on rational numbers, the solution is always a rational number page 8 11. Use closure tables to answer each of the following questions.
Source: mathsmd.com
Before understanding this topic you must know what are whole numbers ? Closure property of rational numbers under subtraction: Add, subtract, and multiply polynomials.
Source: chegg.com
(4) r contains an additive identity element, called zero and usually denoted by 0 or Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; This smallest closed set is called the closure of s (with respect to these operations).
Source: learnzillion.com
4 − 9 = −5. Closure property under subtraction of integers if we subtract any two integers the result is always an integer, so we can say that integers are closed under subtraction. For two rational numbers say x and y the results of addition, subtraction and multiplication operations give a rational number.
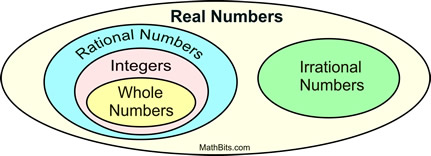Source: mathbitsnotebook.com
Can you try for multiplication and. The set of real numbers is closed under subtraction because a, b ∈ r does imply a − b ∈ r. Let us say ‘a’ and ‘b’ are two integers either positive or negative, their result should always be an integer, i.e (a + b) would always be an integer.
Source: chegg.com
(4) r contains an additive identity element, called zero and usually denoted by 0 or Is the set {0, 1} closed under addition? (4) r contains an additive identity element, called zero and usually denoted by 0 or
Source: brainly.in
This smallest closed set is called the closure of s (with respect to these operations). A set is closed under an operation if the results of that operation always lies in that set. Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication;
Source: slideplayer.com
The set of integers is closed under subtraction. This is a general idea, and. This is known as closure property for subtraction of whole numbers read the following terms and you can further understand this property
Source: youtube.com
As you see, a closed set ($y$ in this definition) is a subset of another set ($x$ in this definition), and the operation may take and give members of $x$ which are not in $y$. The sum we get is 11 which as we know is a whole number. Do you know why division is not under closure.
![Solved] 1.Is The Set Of Rational Expressions Closed Under Subtraction?Explain P(X)/Q(X) - R(X)/S(X) = 2.Is The Set Of Rational Expressions Closed Un… | Course Hero](https://www.coursehero.com/qa/attachment/14590262/ “Solved] 1.Is The Set Of Rational Expressions Closed Under Subtraction?Explain P(X)/Q(X) - R(X)/S(X) = 2.Is The Set Of Rational Expressions Closed Un… | Course Hero”) Source: coursehero.com
Add, subtract, and multiply polynomials. Are polynomials closed under subtraction? This is a general idea, and.
Source: youtube.com
Real numbers are closed under addition and multiplication. Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; (notice also that this set is closed, but does not have an identity and therefore also does not have the inverse property.) 4) the set of natural numbers under addition is not a group , because it does not satisfy all of the group properties:
Source: chegg.com
Add, subtract, and multiply polynomials. A ring is a nonempty set r with two binary operations (usually written as addition and multiplication) such that for all a;b;c 2 r, (1) r is closed under addition: The set of integers is closed under subtraction.
Source: slideplayer.com
For any two rational numbers, say x and y, the results of addition, subtraction and multiplication operations give a rational number. Real numbers are closed under addition and multiplication. The difference between any two positive integers doesn�t always yield a positive integer score.
Source: brainly.com
Can you try for multiplication and. Explanation integers are closed under subtraction which mean that subtraction of integers will also give integers. Therefore, the set of integers under subtraction is not a group!
Source: slideplayer.com
D) the set of natural numbers is not closed under the operation of subtraction because when you subtract one natural number from another, you don’t always get another natural number. The set that is not closed under subtraction is b) z. Use closure tables to answer each of the following questions.
Source: brainly.in
Therefore, the set of integers under subtraction is not a group! Add, subtract, and multiply polynomials. Are polynomials closed under subtraction?
Source: study.com
Now,take any 2 numbers and add them. Which set is closed under subtraction? The set of integers is closed under addition.
Source: brainly.com
Plication, but the set of whole numbers is not closed under subtraction. Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; Real numbers are closed under addition and multiplication.
Source: slideserve.com
Plication, but the set of whole numbers is not closed under subtraction. This closure game is fun. D) the set of natural numbers is not closed under the operation of subtraction because when you subtract one natural number from another, you don’t always get another natural number.
Also Read :
