Since 5 is also an integer we can say that. A set, well defined collection of objects such as numbers, is considered closed under a specific operation if applying that operation to two members of the set will result in.
Which Of The Following Sets Is Closed Under Subtraction. Integers provide closure under subtraction, while whole numbers do not. Which of the following sets is closed under subtraction? They are not closed under subtraction. 4 − 9 = −5.
Solved Which Of The Following Sets Are Closed Under | Chegg.com From chegg.com
Related Post Solved Which Of The Following Sets Are Closed Under | Chegg.com :
The difference between any two rational numbers will always be a rational number, i.e. The set of irrational numbers. Asked 198 days ago|6/14/2021 1:19:45 pm. Often a closure property is introduced as an axiom, which is then usually called the axiom of closure.
Since, if we subtract two integers it will be an integer only.
The set of whole numbers. Subtracting two whole numbers might not make a whole number. Note that closure under an operation depends on both the operation and the set. Which of the following sets is not closed under subtraction? −5 is not a whole number (whole numbers can�t be negative) so: So this is a negative and stir so we see that this set is an operation is not closed.
Source: meritnation.com
For example, the whole numbers are closed under addition, because if Integers provide closure under subtraction, while whole numbers do not. 1 see answer aryan561451 is waiting for your help.
Source: chegg.com
Click an item in the list or group of pictures at the bottom of the problem and. Example 1 = explain closure property under subtraction with the help of given integers 10 and 5. Whole numbers are not closed under subtraction.
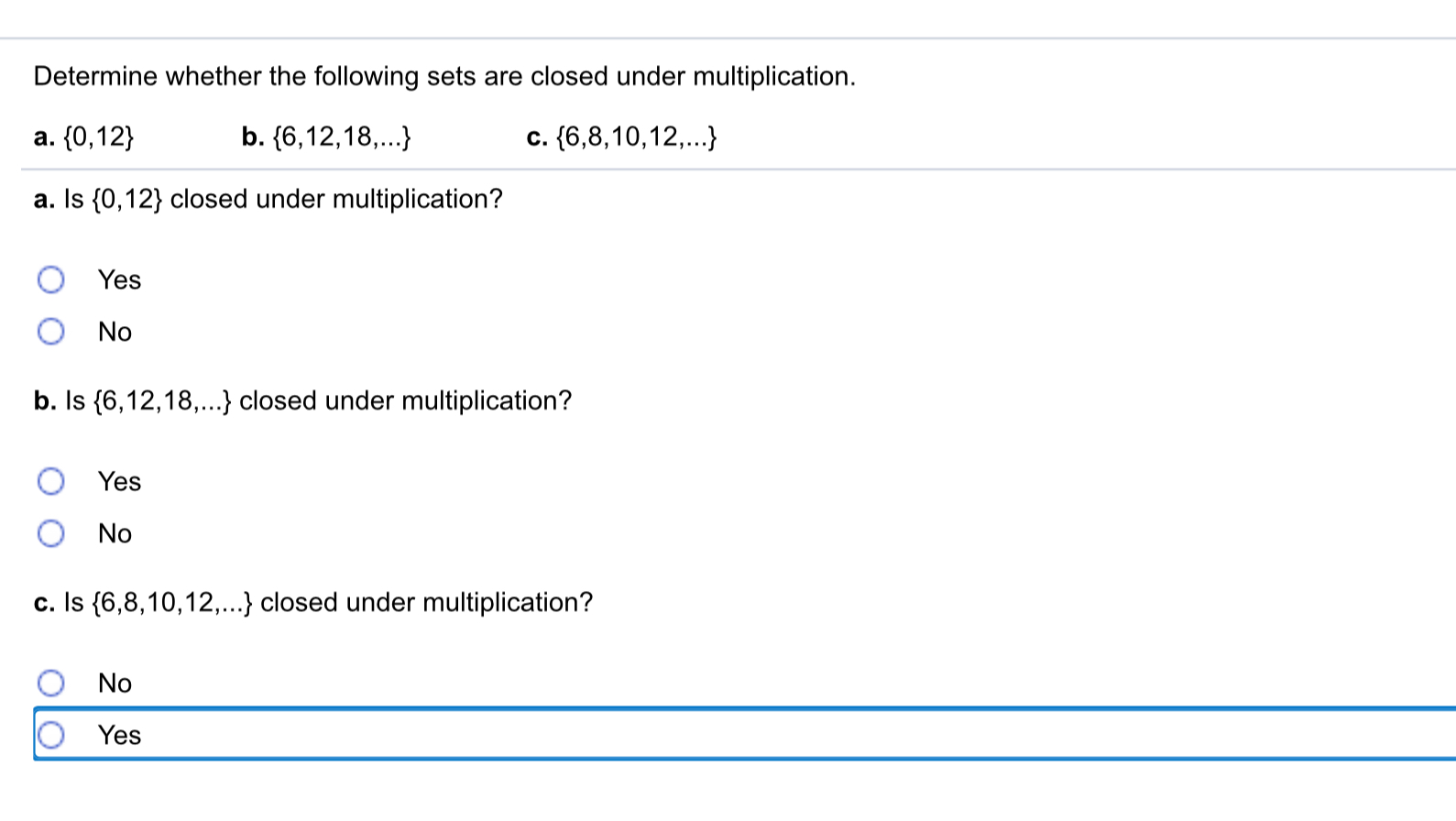Source: chegg.com
If we enlarge our set to be the integers They are closed under subtraction. Set {0, 1} so this set is closed under multiplication.
Source: brainly.com
No.a set is closed under subtraction if when you subtract any two numbers in the set, the answer is always a member of the set.the natural numbers are. The set of whole numbers. I generally see closed under some.
Source: youtube.com
What does being closed under subtraction have to do with it? Given this circumstance, which of the following set of numbers is closed under subtraction? Now, if we subtract these two, if we take a minus b, there should be a positive integer if it�s closed.
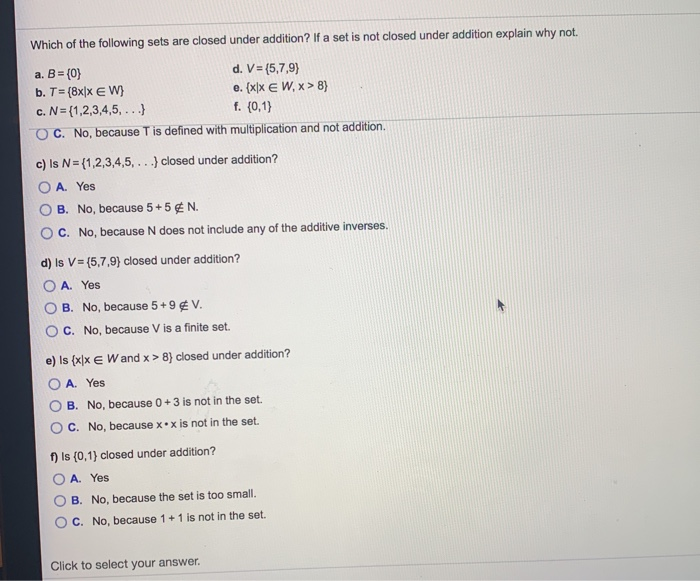Source: chegg.com
So here we have our positive vintages and subjection. The integers are closed under subtraction. The set of natural numbers.
Source: chegg.com
Log in for more information. I} is closed under addition. If a flying operation to any two numbers in the set results in a number of another number in this sense, so we want to determine if are following operations and it sets is closed.
Source: numerade.com
In your notebook, set up the following subtraction in a vertical format and select the correct answer. Integers provide closure under subtraction, while whole numbers do not. Whole numbers are (1,2,3,4,5.) now,take any 2 numbers and add them.
Source: chegg.com
Addition division multiplication subtraction none determine whether the set. Closure property of rational numbers under multiplication: Is closed under addition, subtraction.
Source: chegg.com
Since, if we subtract two integers it will be an integer only. This smallest closed set is called the closure of s (with respect to these operations). They are closed under subtraction.
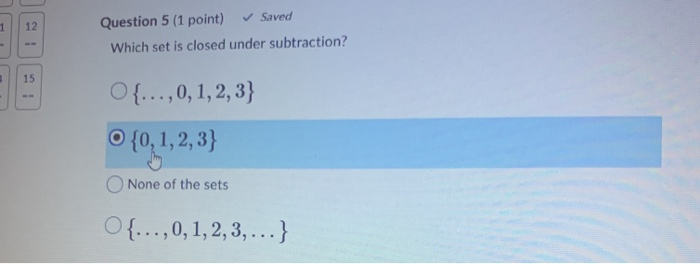Source: chegg.com
They are not closed under subtraction. Which set is closed under subtraction? So, closed under subtraction means if we subtract two numbers of a set than it must belong to that set.
Source: learnzillion.com
Which of the following sets is closed under subtraction? For example, the closure under subtraction of the set of natural numbers, viewed as a subset of the real numbers, is the set of integers. A set of elements is closed under an operation if, when you apply the operation to elements of the set, you always get another element of the set.
Source: brainly.com
The sum we get is 11 which as we know is a whole number. The set of rational numbers. In mathematics, a subset of a given set is closed under an operation of the larger set if performing that operation on members of the subset always produces a member of that subset.
Source: youtube.com
Add your answer and earn points. At some point, people were confronted with the problem of having to divide one thing among more than one person. Subtracting two whole numbers might not make a whole number.
Source: brainly.in
Integers provide closure under subtraction, while whole numbers do not. But we got to minus three, which is equal to negative one. 4) every element of the set has an inverse under the operation that is also an element of the set.
Source: study.com
Which set is closed under subtraction? They are closed under subtraction. A set of elements is closed under an operation if, when you apply the operation to elements of the set, you always get another element of the set.
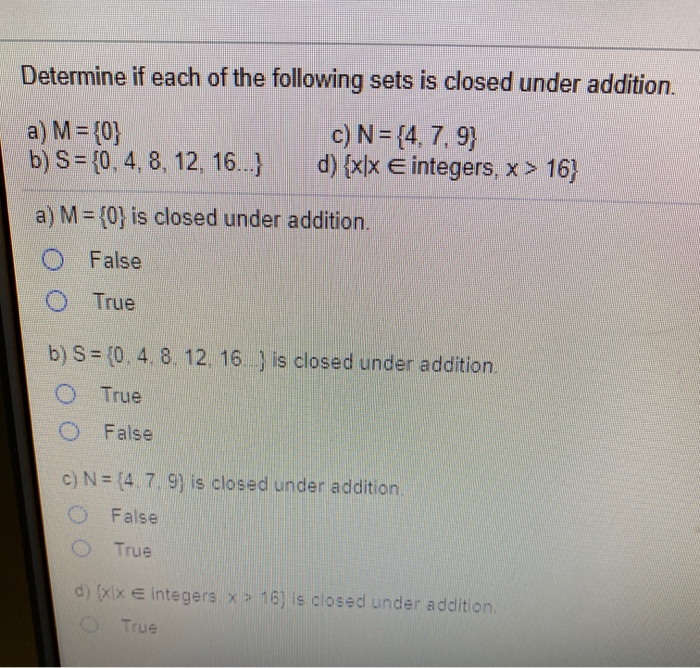Source: chegg.com
Is the set {0, 1} closed under addition? That’s true in certain cases.(namely, multiplying some quantity x by a n. 3) the set has an identity element under the operation that is also an element of the set.
Source: bartleby.com
Which of the following sets is not closed under subtraction? Addition division multiplication subtraction none determine whether the set. So, closed under subtraction means if we subtract two numbers of a set than it must belong to that set.
Source: slideplayer.com
This smallest closed set is called the closure of s (with respect to these operations). So this is a negative and stir so we see that this set is an operation is not closed. We have our integer on addition and subtraction.
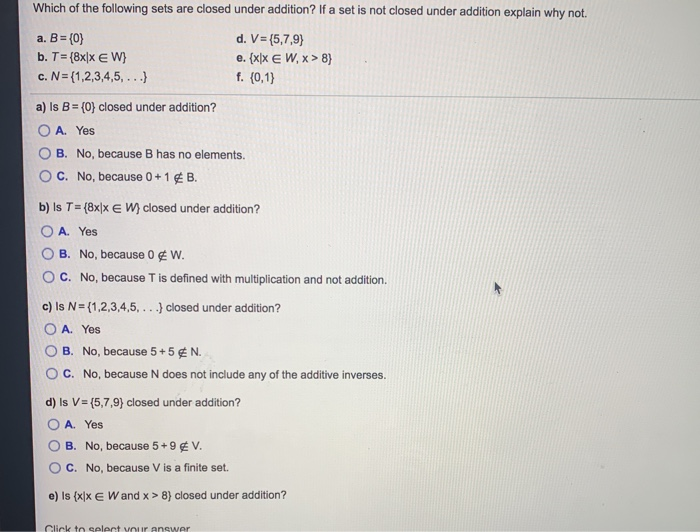Source: chegg.com
I generally see closed under some. Given this circumstance, which of the following set of numbers is closed under subtraction? Okay, i�m for part b.
Also Read :
