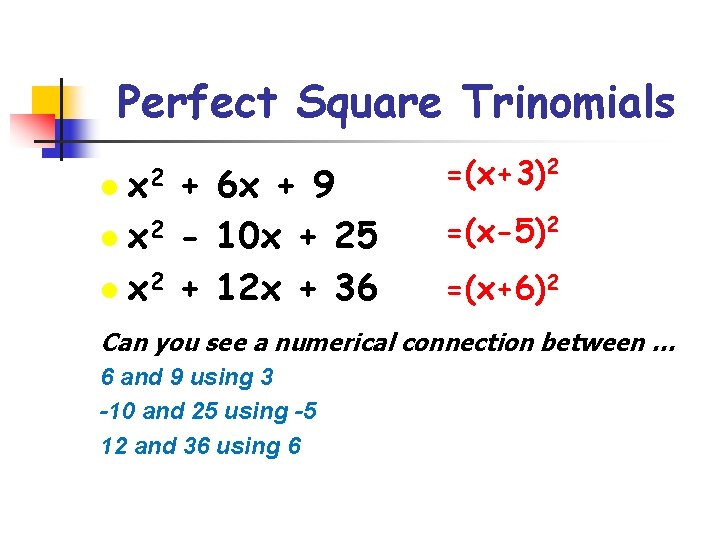
(x + n)^2 = x^2 + 2*n + n^2. The middle term must be twice the product of the square roots of the first and last terms.
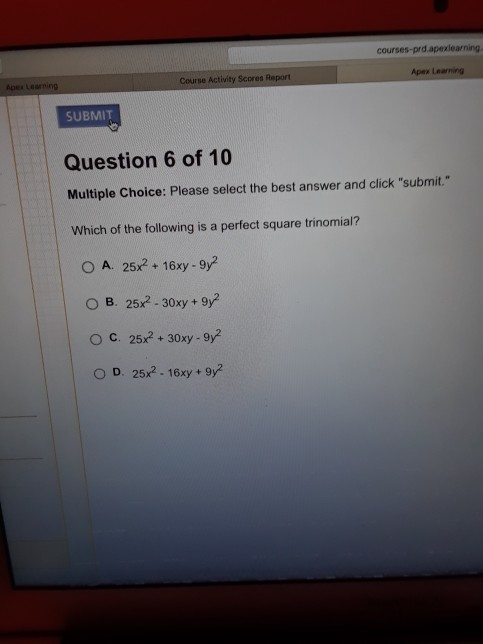
Which Of The Following Is A Perfect Square Trinomial. Given the following perfect square trinomial, fill in the missing term. The following table shows examples of perfect square trinomials in different forms. 1 which of the following is an example of a perfect. A perfect square trinomial is a trinomial that can be written as the square of a binomial.
Completing The Square For Conic Sections The Aim From slidetodoc.com
Related Post Completing The Square For Conic Sections The Aim :
How to factor a perfect square trinomial? Which of the following is not a perfect square trinomial? Otherwise the given trinomial is not a perfect square. Given the following perfect square trinomial, fill in the missing term.
A quadratic expression is an expression whose highest exponent in the v.
So it must involve the square root of which is x and it must also involve the square Recall that when a binomial is squared, the result is the square of the first term added to twice the product of the two terms and the square of the last term. When the binomial terms are multiplied by itself, then the resulting term is called a perfect square trinomial. X 2 + 18x + 81 Factor the following perfect square trinomial using the rule(b/2) 2: In the example here, 2*n = b = 24.
Source: chegg.com
If we are able to write the given trinomial in the above form, then it is perfect square. A quadratic expression is an expression whose highest exponent in the v. Let assume that, a function f(x) = ax 2 +bx+c is said to be a perfect square trinomial if it has double roots.
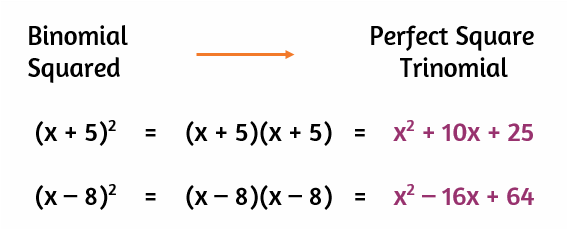Source: katesmathlessons.com
To test whether the given trinomial is a perfect square, we should try to write the trinomial in the form of. When the binomial terms are multiplied by itself, then the resulting term is called a perfect square trinomial. 16 is a perfect square of 4 times 4, and 9 is a perfect square of 3 times 3.
Source: basic-mathematics.com
If we are able to write the given trinomial in the above form, then it is perfect square. Ax^2 + bx + c. Once we have identified a perfect square trinomial, we follow the following steps to factor:
Source: slideplayer.com
Once we have identified a perfect square trinomial, we follow the following steps to factor: For example, if (a + 2) is a binomial, then the perfect square trinomial is obtained by multiplying (a+2) and (a+2), which gives a 2 + 4a + 4. Log in for more information.
Source: brainly.com
A perfect square trinomial is formed by multiplying two binomials, which are one and the same. X 2 + 18x + 81 Solved example of perfect square trinomial.
Source: onlinemathlearning.com
Therefore, a perfect square trinomial can be defined as an expression that is obtained by squaring a binomial The components, a and b , that make up the perfect square trinomial can be constants. X 2 + 18x + 81
Source: ck12.org
To test whether the given trinomial is a perfect square, we should try to write the trinomial in the form of. A perfect square trinomial is a special type of trinomial. A perfect square trinomial is formed by multiplying two binomials, which are one and the same.
Source: topptutors.blogspot.com
You�ve solved a perfect square trinomial! The square root of x2 is x, the square root of 36 is 6, and 2 times x (which is the same as 1) times 6. The components, a and b , that make up the perfect square trinomial can be constants.
Source: slidetodoc.com
It means that, if f(a)= 0, f’(a) =0, but f”(a) is not zero, then the trinomial f(x) is said to be a perfect square. An expression is claimed to a perfect square trinomial if it takes the type ax2 + bx + c and satisfies the problem b2 = 4ac. Given the following perfect square trinomial, fill in the missing term.
Source: study.com
The following table shows examples of perfect square trinomials in different forms. For this case, we have that by definition, a perfect square trinomial, is a polynomial of three terms (also called trinomial) that results from squaring a binomial. Log in for more information.
Source: brainly.com
👉 learn how to find the value c that completes the square in a quadratic expression. X 2 + 18x + 81 Similarly, a binomial is an expression composed of two terms.
Source: cuemath.com
Therefore, a perfect square trinomial can be defined as an expression that is obtained by squaring a binomial What square number must we add? X2 16x + ____ 24 36 54 64.
Source: youtube.com
Once we have identified a perfect square trinomial, we follow the following steps to factor: Which of the following or properties of a perfect square trinomial? In the example here, 2*n = b = 24.
Source: quizizz.com
For this case, we have that by definition, a perfect square trinomial, is a polynomial of three terms (also called trinomial) that results from squaring a binomial. Recall that when a binomial is squared, the result is the square of the first term added to twice the product of the two terms and the square of the last term. So n = 12, and c = n^2 = 144.
Source: slideplayer.com
Identify the square numbers in the first and last terms of the trinomial. The first and last terms must be perfect squares; Examine whether the middle term is positive or negative.
Source: chegg.com
Let’s take a look at the steps. 16 is a perfect square of 4 times 4, and 9 is a perfect square of 3 times 3. That only one of two factors can be squared to give you the trinomial.
Source: youtube.com
When the binomial terms are multiplied by itself, then the resulting term is called a perfect square trinomial. (x + n)^2 = x^2 + 2*n + n^2. A perfect square trinomial is a trinomial that can be written as the square of a binomial.
Source: brainly.com
X2 16x + ____ 24 36 54 64. 👉 learn how to find the value c that completes the square in a quadratic expression. A perfect square trinomial is a special type of trinomial.
Source: andymath.com
Which of the following factors gives a product of n 2 + 7n + 6? Once we have identified a perfect square trinomial, we follow the following steps to factor: The square root of x2 is x, the square root of 36 is 6, and 2 times x (which is the same as 1) times 6.
Source: youtube.com
To test whether the given trinomial is a perfect square, we should try to write the trinomial in the form of. Let’s take a look at the steps. If we are able to write the given trinomial in the above form, then it is perfect square.
Also Read :
