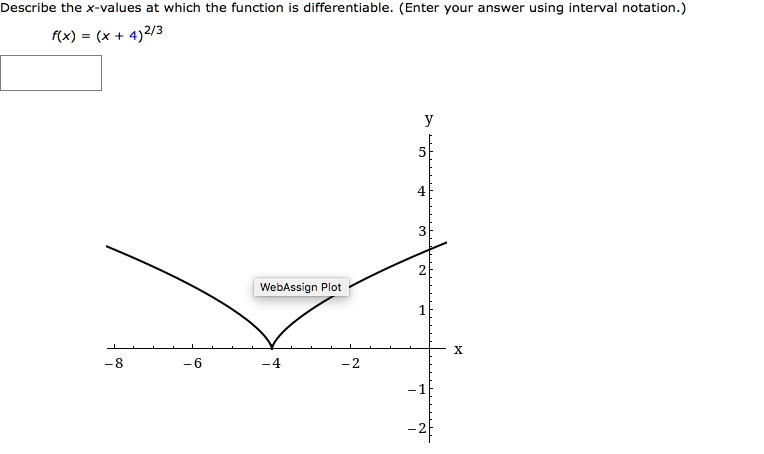
The function is differentiable from the left and right. Its domain is the set { x ∈ r:
Describe The X Values At Which The Function Is Differentiable. But for modulus function at x=0, no unique tangent can be drawn. Piecewise functions may or may not be differentiable on their domains. Definition function f is differentiable at x=a if and only if f�(a) exists. A function f f f is differentiable at a point x 0 x_0 x 0 if.
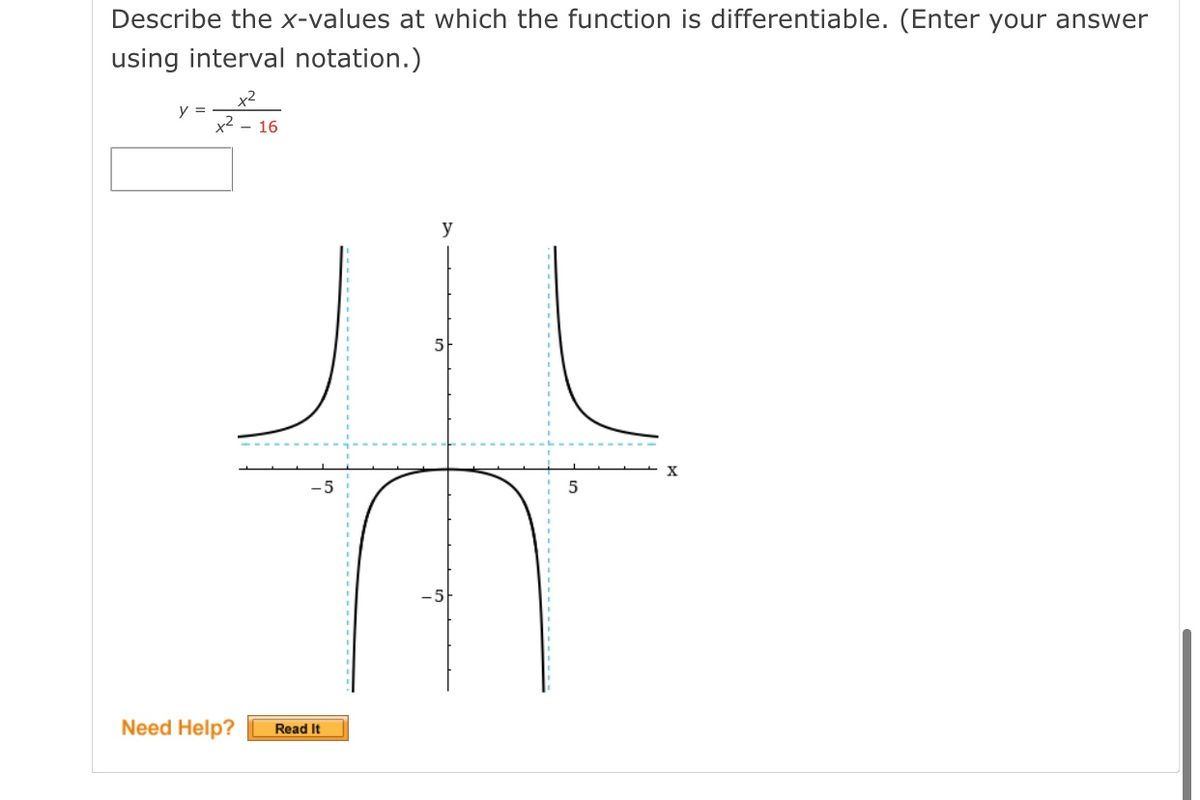Answered: Describe The X-Values At Which The… | Bartleby From bartleby.com
Related Post Answered: Describe The X-Values At Which The… | Bartleby :
- f f f is continuous at x 0 x_0 x 0 and 2) the slope of tangent at point x 0 x_0 x 0 is well defined. F ′ ( x) = lim δ x → 0 ( x + δ x) 2 − 4 − ( x 2 − 4) δ x = lim . Otherwise, it�s not differentiable at x=a. At point c c c on the interval [a, b] [a, b] [a, b] of the function f (x) f(x) f (x), where the function is.
Briefly, differentiable means can be differentiated and that mean has a derivative.
Let ( ), 0, 0 > − ≤ = x x x x f x first we will check to prove continuity at x = 0 The derivative function, denoted by , is the function whose domain consists of those values of such that the following limit exists: F ′ ( x) f� (x) f ′ ( x) using the limit definition. So this looks like we are both continuous and differentiable. Hence, |x| is not differentiable at x=0. Let’s consider some piecewise functions first.
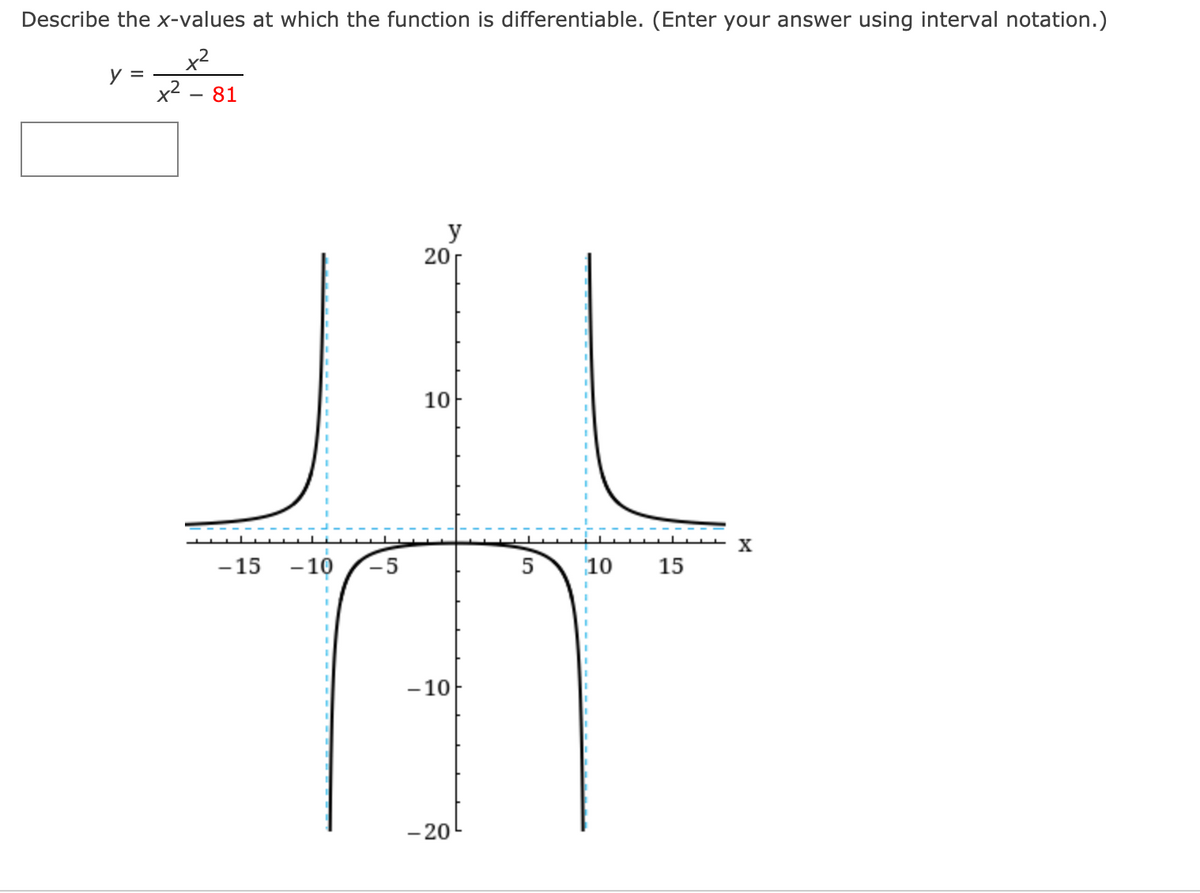Source: bartleby.com
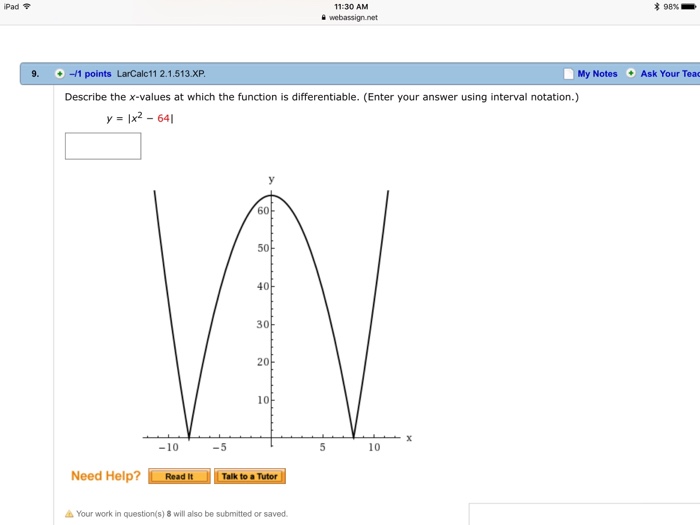
Hence, |x| is not differentiable at x=0. F ′ ( x) f� (x) f ′ ( x) using the limit definition. The function is differentiable for all x # +64.
Source: chegg.com
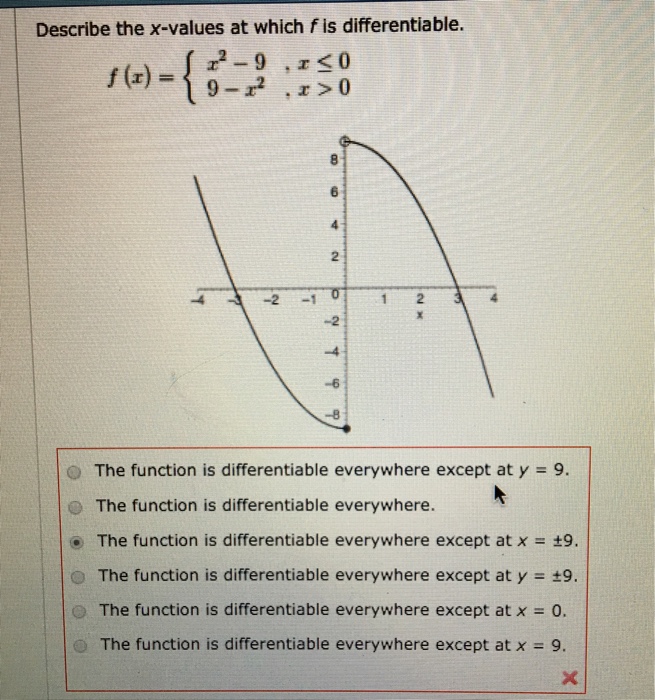
Its domain is the set { x ∈ r: We�ve got the study and writing resources you need for your assignments. More generally, a function is said to be differentiable on if it is differentiable at every point in an open set , and a differentiable function is one in.
Source: bartleby.com
For example, the function f ( x) = 1 x only makes sense for values of x that are not equal to zero. The function is differentiable for all x # +64. The derivative function, denoted by , is the function whose domain consists of those values of such that the following limit exists:
Source: chegg.com
For example, the function f ( x) = 1 x only makes sense for values of x that are not equal to zero. Function g below is not differentiable at x = 0 because there is no tangent to the graph at x = 0.(try to draw a tangent at x=0!) function h below is not differentiable at x = 0 because there is a jump in the value of the function and also the function is not defined therefore not continuous at x = 0. (enter your answer using interval notation.
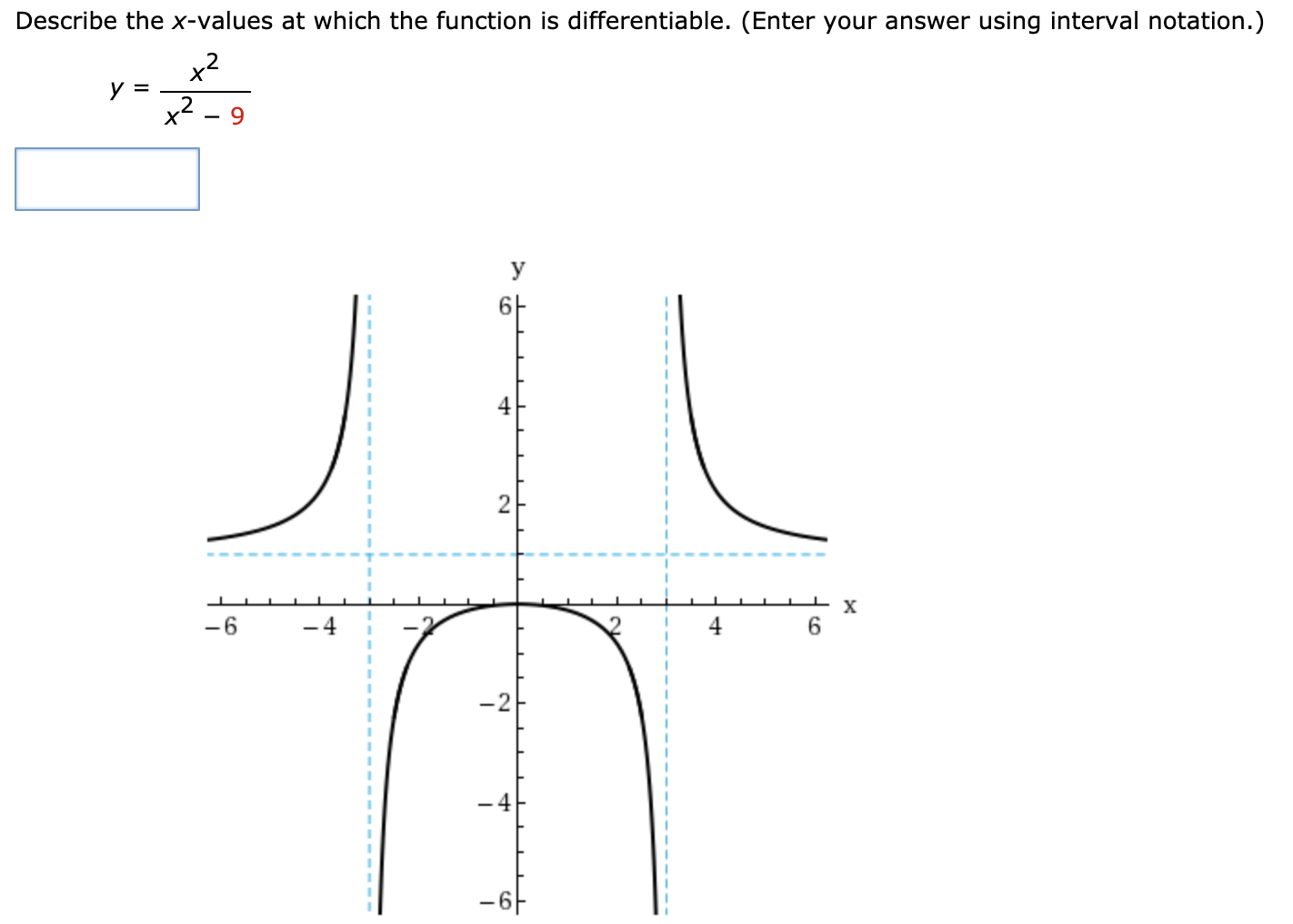Source: chegg.com
The function is differentiable for all x + +8. To be differentiable at a point x = c, the function must be continuous, and we will then see if it is differentiable. Function g below is not differentiable at x = 0 because there is no tangent to the graph at x = 0.(try to draw a tangent at x=0!) function h below is not differentiable at x = 0 because there is a jump in the value of the function and also the function is not defined therefore not continuous at x = 0.
Source: chegg.com
F ′ ( x) = lim δ x → 0 ( x + δ x) 2 − 4 − ( x 2 − 4) δ x = lim . As in the case of the existence of limits of a function at x 0, it follows that. At point c c c on the interval [a, b] [a, b] [a, b] of the function f (x) f(x) f (x), where the function is.
Source: chegg.com
Otherwise, it�s not differentiable at x=a. For example, the function f ( x) = 1 x only makes sense for values of x that are not equal to zero. Definition function f is differentiable at x=a if and only if f�(a) exists.
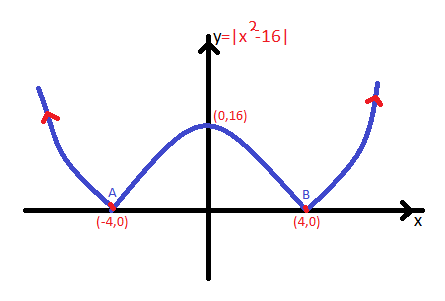Source: study.com
Function j below is not differentiable at x. The function is differentiable from the left and right. But for modulus function at x=0, no unique tangent can be drawn.
Source: chegg.com
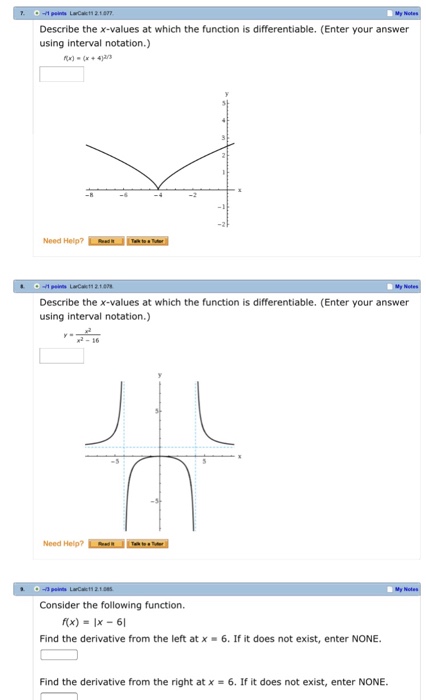
The function is differentiable for all x + +8. To be differentiable at a certain point, the function must first of all be defined there! As we head towards x = 0 the function moves up and down faster and faster, so we cannot find a value it is heading towards.
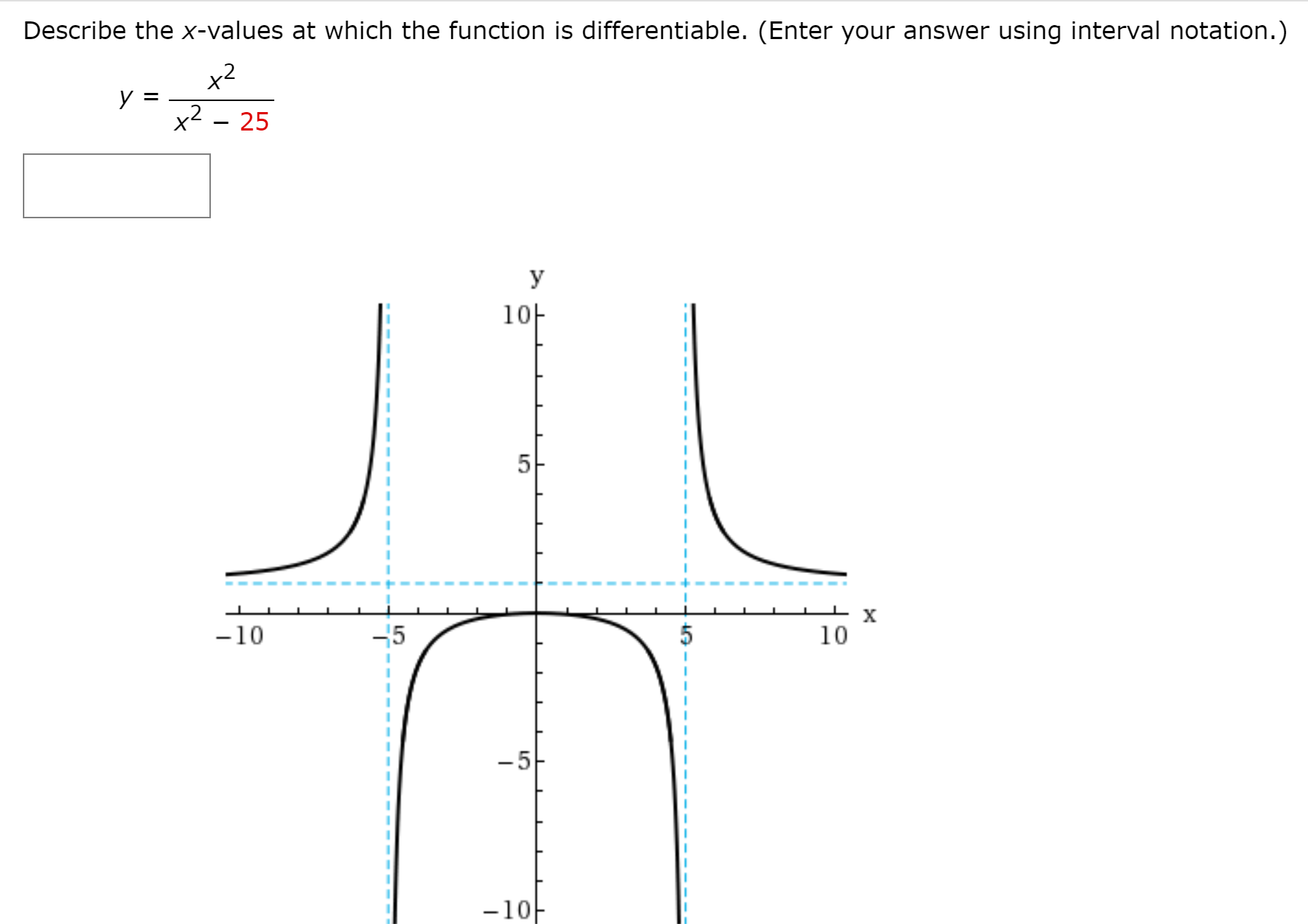Source: bartleby.com
The function is differentiable for all x # +64. More generally, a function is said to be differentiable on if it is differentiable at every point in an open set , and a differentiable function is one in. (enter your answer using interval notation.
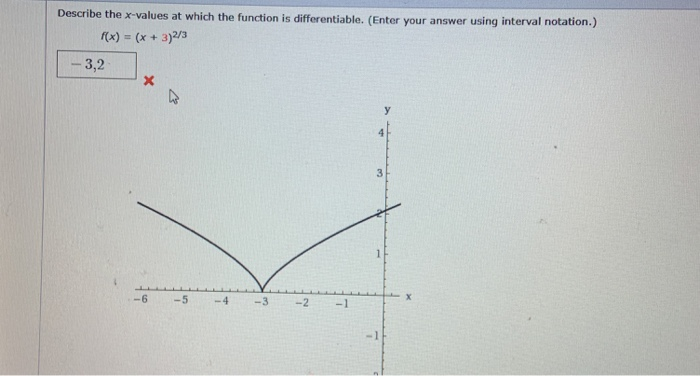Source: chegg.com
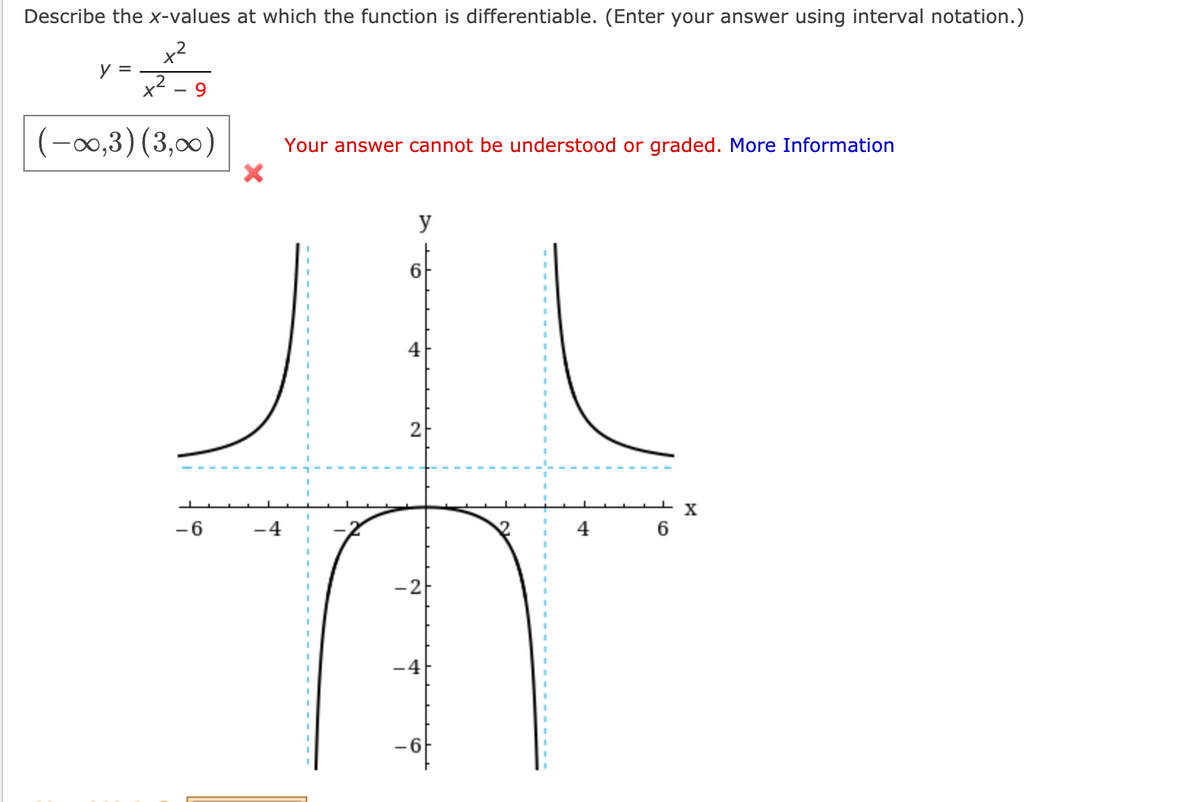
If any one of the condition fails then f� (x) is not differentiable at x 0. Hence the function f (x) = ∣∣x2 − 9∣∣ is differentiable everywhere with the exception of x = ± 3. Its domain is the set { x ∈ r:
Source: chegg.com
F ′ ( x) = lim δ x → 0 f ( x + δ x) − f ( x) δ x for x ≤ 0: A function f f f is differentiable at a point x 0 x_0 x 0 if. As we head towards x = 0 the function moves up and down faster and faster, so we cannot find a value it is heading towards.
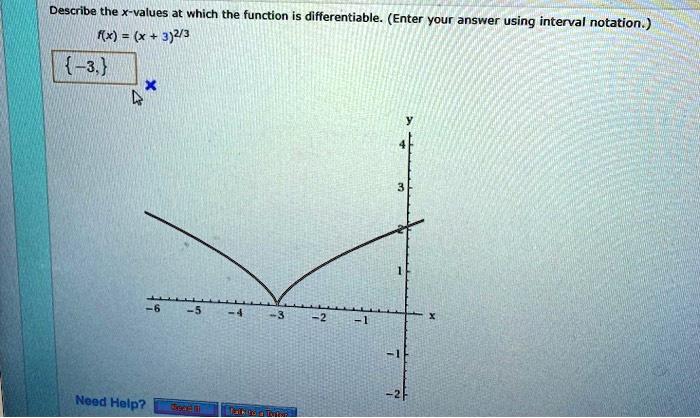Source: numerade.com
Briefly, differentiable means can be differentiated and that mean has a derivative. F ′ ( x) = lim δ x → 0 f ( x + δ x) − f ( x) δ x for x ≤ 0: More generally, a function is said to be differentiable on if it is differentiable at every point in an open set , and a differentiable function is one in.
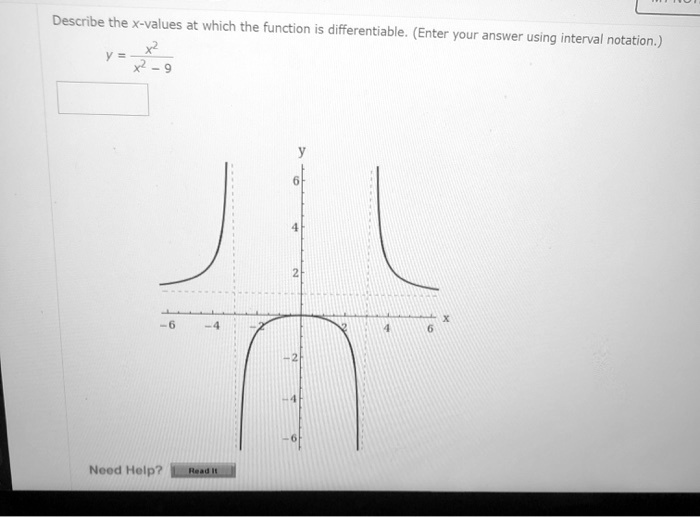Source: itprospt.com
( 0, ∞) \left ( 0,\infty \right) ( 0, ∞) let�s try to find. F(x) is differentiable everywhere except at x = 0. If any one of the condition fails then f� (x) is not differentiable at x 0.
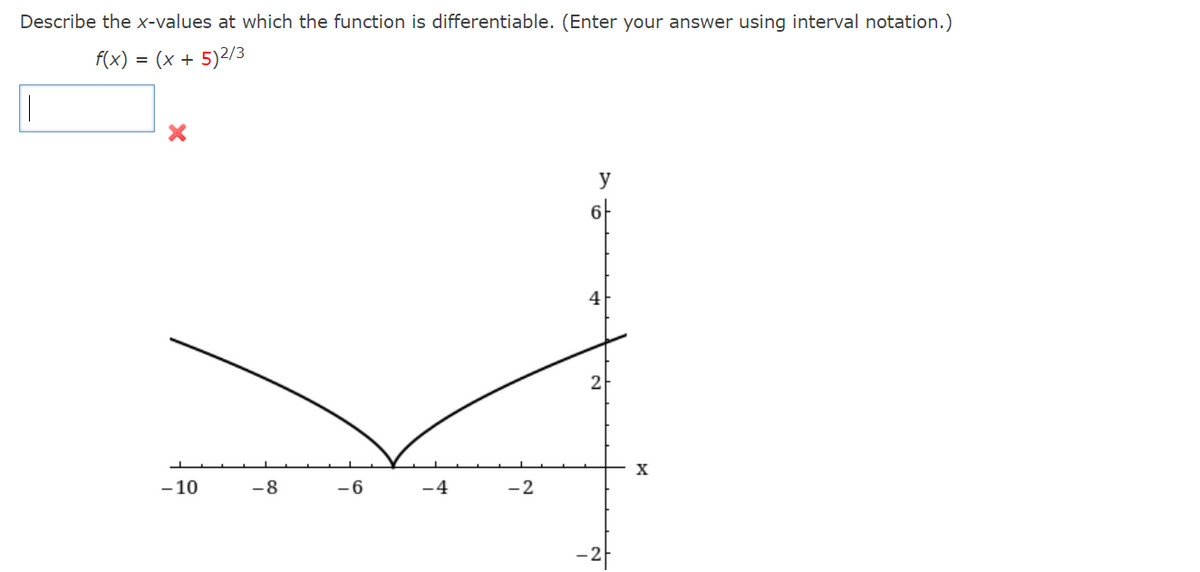Source: bartleby.com
If any one of the condition fails then f� (x) is not differentiable at x 0. A function f f f is differentiable at a point x 0 x_0 x 0 if. Let ( ), 0, 0 > − ≤ = x x x x f x first we will check to prove continuity at x = 0
Source: chegg.com
A function is said to be differentiable at x=a, if a unique tangent passes through that point. Piecewise functions may or may not be differentiable on their domains. We�ve got the study and writing resources you need for your assignments.
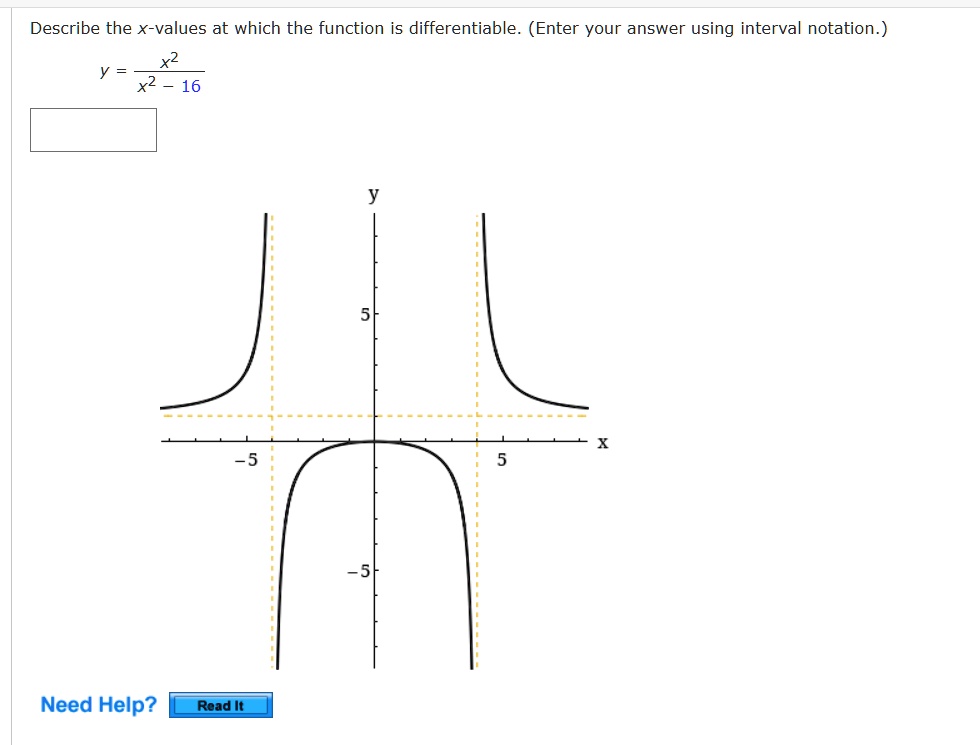Source: numerade.com
The derivative function, denoted by , is the function whose domain consists of those values of such that the following limit exists: At x=0 the function is not defined so it makes no sense to ask if they are differentiable there. If any one of the condition fails then f� (x) is not differentiable at x 0.
Source: numerade.com
Piecewise functions may or may not be differentiable on their domains. As in the case of the existence of limits of a function at x 0, it follows that. The derivative function, denoted by , is the function whose domain consists of those values of such that the following limit exists:
Source: chegg.com
The noun differentiation is the act or process of differentiating, hence, the act or process of finding a derivative. A function f f f is differentiable at a point x 0 x_0 x 0 if. Briefly, differentiable means can be differentiated and that mean has a derivative.
Source: bartleby.com
Hence, |x| is not differentiable at x=0. To be differentiable at a point x = c, the function must be continuous, and we will then see if it is differentiable. (enter your answer using interval notation.
Also Read :
